Участник:MarchenkovSS

Марченков Сергей Серафимович

Марченков Сергей Серафимович — доктор физико-математических наук, профессор.

Области научных интересов

Теория функциональных систем

Функциональные системы, состоящие из функций многозначной логики, автоматных, рекурсивных и непрерывных функций, вместе с операцией суперпозиции и некоторыми другими операциями. Вопросы классификации, полноты и существования базисов. Вопросы предикатного описания замкнутых классов для функций многозначной логики.

Теория алгоритмов

Вопросы классификации рекурсивных функций, сложности вычисления функций на абстрактных вычислительных устройствах различного вида, алгоритмической разрешимости логических и логико-арифметических теорий, строения полурешеток степеней неразрешимости и вычислимых нумераций.

Теория автоматов

Вопросы классификации рекурсивных функций, сложности вычисления функций на абстрактных вычислительных устройствах различного вида, алгоритмической разрешимости логических и логико-арифметических теорий, строения полурешеток степеней неразрешимости и вычислимых нумераций.

Лекционные курсы

• Дополнительные главы дискретной математики (II поток)
• Однородные функции
• Операторы замыкания в многозначной логике
• Основы теории алгоритмов
• Предикатное определение замкнутых классов
• Предполные классы многозначной логики
• Функциональные системы
• Частичные булевы функции
• Элементарные рекурсивные функции

Избранные публикации

1. Об одном классе неполных множеств // Математические заметки. - 1976. - Т. 20, N 4. - C. 473-478.
2. Об одном методе анализа суперпозиций непрерывных функций // Проблемы кибернетики, вып. 37. - 1980. - С. 5-17.
3. Однородные алгебры // Проблемы кибернетики, вып. 39. - 1982. - С. 85-106.
4. Классификация алгебр со знакопеременной группой автоморфизмов // Математические вопросы кибернетики, вып. 2. - 1989. - С. 100-122.
5. Конечные начальные сегменты верхней полурешетки конечно-автоматных степеней // Дискретная математика. - 1989. - Т. 1, N 3. - C. 96-103.
6. Простые примеры базисов по суперпозиции в классе функций, элементарных по Кальмару // Banach Center Publication. - 1989. - V. 25. - P. 119-126.
7. О представлении словарных предикатов из арифметической иерархии // Дискретная математика. - 1990. - Т. 2, N 1. - C. 87-93.
8. О равномерном

-разложении булевых функций // Дискретная математика. - 1990. - Т. 2, N 3. - C. 29-41.

1. Базисы по суперпозиции в классах рекурсивных функций // Математические вопросы кибернетики, вып. 3. - 1991. - С. 115-139.
2. О классах Слупецкого в системах

// Дискретная математика. - 1992. - Т. 4, N 3. - C. 135-148.

1. Предполнота замкнутых классов в 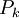$P_k$: предикатный подход // Математические вопросы кибернетики, вып. 6. - 1996. - С. 117-132.

-классификация функций многозначной логики // Дискретная математика. - 1997. - Т. 9, N 3. - С. 125-152.

1. Инварианты классов Поста // Фундаментальная и прикладная математика. - 1998. - Т. 4, N 4. - С. 1385-1404.

-классификация идемпотентных функций многозначной логики // Дискретный анализ и исследование операций. Серия 1. - 1999. - Т. 6, N 1. - С. 19-43.

1. О суперпозициях непрерывных функций, заданных на бэровском пространтстве // Математические заметки. - 1999. - Т. 66, N 5. - С. 696-705.
2. Замкнутые классы булевых функций. // М.: Наука, 2000, 126 стр.
3. О невозможности получения

-местных непрерывных функций из -местных с помощью некоторых непрерывных операторов. // Математический сборник. - 2001. - Т. 192, N 6. - С. 71-88.

-классификация функций трехзначной логики. // М.:Физматлит. 2001, 80 стр

1. Элементарные рекурсивные функции. // М.: МЦНМО, 2003, 112 стр.
2. О сложности возвратных последовательностей. // Дискретная математика. - 2003. - Т. 15, Т 2. - С. 52-62.