Предполные классы многозначной логики — различия между версиями
Root (обсуждение | вклад) (Новая страница: «Полугодовой спецкурс. Лектор — профессор Марченков Сергей Серафимович. == Программа к…») |
(нет различий)
|
Версия 18:46, 31 октября 2013
Полугодовой спецкурс. Лектор — профессор Марченков Сергей Серафимович.
Программа курса
Предикаты на множестве Невозможно разобрать выражение (Преобразование в PNG прошло с ошибкой — проверьте правильность установки latex и dvips (или dvips + gs + convert)): E_k . Отношение сохранения предиката функцией. Предикатное описание классов Невозможно разобрать выражение (Преобразование в PNG прошло с ошибкой — проверьте правильность установки latex и dvips (или dvips + gs + convert)): T_0, T_1, S, M, L .
Семейства предикатов P, O, L, E, C, B. Замкнутость семейств P, O, L, E, C, B относительно операции декартовой степени. Замкнутость семейств E, C, B относительно операции взятия полного прообраза. Соотношение между классами функций Невозможно разобрать выражение (Преобразование в PNG прошло с ошибкой — проверьте правильность установки latex и dvips (или dvips + gs + convert)): \rm{Pol}(\rho)
и Невозможно разобрать выражение (Преобразование в PNG прошло с ошибкой — проверьте правильность установки latex и dvips (или dvips + gs + convert)): \rm{Pol}(\rho^l)
.
Предполнота классов типа P.
Предполнота классов типа O и E.
Класс функций, линейных по простому модулю. Предполнота классов типа L.
Предполнота классов типа C.
Леммы о трех наборах и о квадрате. Класс Слупецкого. Предполнота классов типа B.
Однородные функции. Примеры однородных функций. Построение конечного базиса в классе однородных функций.
Литература
- Rosenberg I.G. Über die funktionale Vollständigkeit in der mehrvertigen Logiken // Rozpravy Československě Akad. Věd. Řada Math. Přir. Věd. Praha. — 1970. — Bd. 80. — S. 3—93
- Яблонский С.В., Гаврилов Г.П., Набебин А.А. Анализ и синтез схем в многозначных логиках. Часть I. М.: Из-во МЭИ, 1989.
- Яблонский С.В., Гаврилов Г.П., Набебин А.А. Предполные классы в многозначных логиках. М.: Из-во МЭИ, 1997.
- Марченков С.С. Предполнота замкнутых классов в
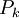 : предикатный подход // Математические вопросы кибернетики, вып. 6. — 1996. — С. 117—132.
: предикатный подход // Математические вопросы кибернетики, вып. 6. — 1996. — С. 117—132.
- Буевич В.А. Вариант доказательства критерия полноты для функций Невозможно разобрать выражение (Преобразование в PNG прошло с ошибкой — проверьте правильность установки latex и dvips (или dvips + gs + convert)): k
-значной логики // Дискретная математика. — 1996. — Т. 8, N 4. — С. 11—36.
- Марченков С.С. Однородные алгебры // Проблемы кибернетики, вып. 39. — 1982. — С. 85—106.
Ссылки
- Программа курса (pdf)