Предикатное определение замкнутых классов — различия между версиями
Root (обсуждение | вклад) (Новая страница: «Полугодовой спецкурс. Лектор — профессор Марченков Сергей Серафимович. == Программа к…») |
Root (обсуждение | вклад) (→Программа курса) |
||
| Строка 3: | Строка 3: | ||
== Программа курса == | == Программа курса == | ||
| − | Предикаты на множестве | + | Предикаты на множестве E_k. Диагонали. Операции конъюнкции и |
проектирования. Формулы с предикатами. Операция замыкания, замкнутые классы | проектирования. Формулы с предикатами. Операция замыкания, замкнутые классы | ||
предикатов. | предикатов. | ||
| Строка 10: | Строка 10: | ||
свойства функторов Pol, Inv. | свойства функторов Pol, Inv. | ||
| − | Соответствия Галуа. Замыкания Галуа. Совпадение замкнутых классов | + | Соответствия Галуа. Замыкания Галуа. Совпадение замкнутых классов F и |
| − | Pol(Inv( | + | Pol(Inv(F)). |
| − | Совпадение замкнутых классов | + | Совпадение замкнутых классов R и Inv(Pol(R)). |
Минимальные классы и минимальные предикаты. Эквивалентные определения | Минимальные классы и минимальные предикаты. Эквивалентные определения | ||
| − | минимальных предикатов. Минимальность булевых предикатов | + | минимальных предикатов. Минимальность булевых предикатов x=0, x=1, x\ne y, x\le y, x_1+x_2=x_3+x_4. |
Операции декартовой степени и взятия полного прообраза, перестановочность | Операции декартовой степени и взятия полного прообраза, перестановочность | ||
с операциями конъюнкции и проектирования. Сохранение минимальности предиката | с операциями конъюнкции и проектирования. Сохранение минимальности предиката | ||
при операциях декартовой степени и взятия полного прообраза. Минимальность | при операциях декартовой степени и взятия полного прообраза. Минимальность | ||
| − | предиката | + | предиката \tau_k. |
Критерий определяемости замкнутого класса конечным числом предикатов. | Критерий определяемости замкнутого класса конечным числом предикатов. | ||
| − | Предикатное определение классов | + | Предикатное определение классов U, K, D, O^m, I^m. |
| − | Теория Галуа для симметрической полугруппы | + | Теория Галуа для симметрической полугруппы {\bf T}_k и симметрической |
| − | группы | + | группы {\bf S}_k. |
== Литература == | == Литература == | ||
Версия 12:33, 30 января 2014
Полугодовой спецкурс. Лектор — профессор Марченков Сергей Серафимович.
Программа курса
Предикаты на множестве E_k. Диагонали. Операции конъюнкции и проектирования. Формулы с предикатами. Операция замыкания, замкнутые классы предикатов.
Отношение сохранения предиката функцией. Функторы Pol и Inv. Основные свойства функторов Pol, Inv.
Соответствия Галуа. Замыкания Галуа. Совпадение замкнутых классов F и Pol(Inv(F)).
Совпадение замкнутых классов R и Inv(Pol(R)).
Минимальные классы и минимальные предикаты. Эквивалентные определения минимальных предикатов. Минимальность булевых предикатов x=0, x=1, x\ne y, x\le y, x_1+x_2=x_3+x_4.
Операции декартовой степени и взятия полного прообраза, перестановочность с операциями конъюнкции и проектирования. Сохранение минимальности предиката при операциях декартовой степени и взятия полного прообраза. Минимальность предиката \tau_k.
Критерий определяемости замкнутого класса конечным числом предикатов. Предикатное определение классов U, K, D, O^m, I^m.
Теория Галуа для симметрической полугруппы {\bf T}_k и симметрической группы {\bf S}_k.
Литература
- Боднарчук В.Г., Калужнин Л.А., Котов В.Н., Ромов Б.А. Теория Галуа для алгебр Поста // Кибернетика. — 1969. — N 3. — С. 1—10; N 5. — С. 1—9.
- Марченков С.С. Замкнутые классы булевых функций. М.: Наука, 2000.
- Марченков С.С. Предполнота замкнутых классов в
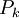: предикатный подход // Математические вопросы кибернетики, вып. 6. — 1996. — С. 117—132.
Ссылки
- Программа курса (pdf)
